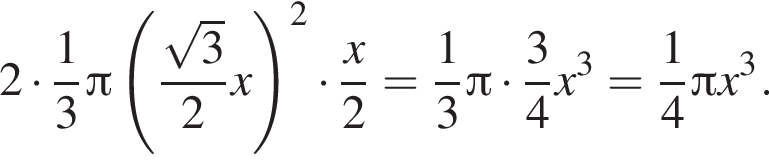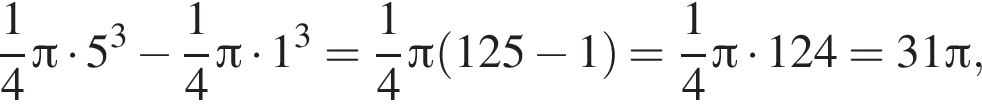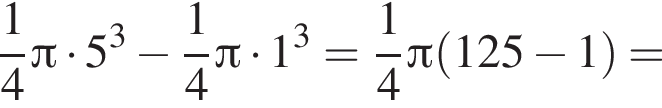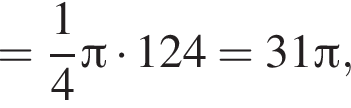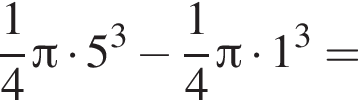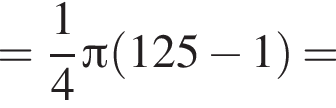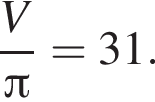Если 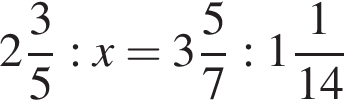 — верная пропорция, то число x равно:
— верная пропорция, то число x равно:
Одна из сторон прямоугольника на 6 см длиннее другой, а его площадь равна 112 см2. Уравнение, одним из корней которого является длина меньшей стороны прямоугольника, имеет вид:
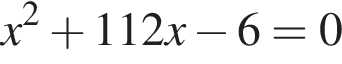
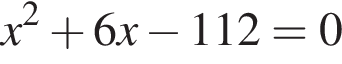
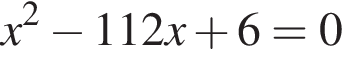
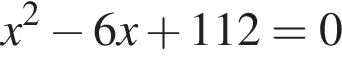
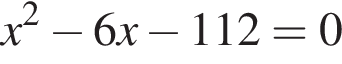
Даны дроби 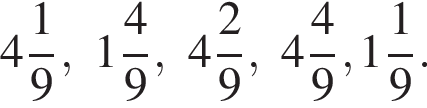 Укажите дробь, которая равна дроби
Укажите дробь, которая равна дроби ![]()
Сумма всех натуральных решений неравенства 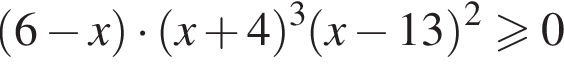 равна:
равна:
Если 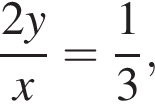 то значение выражения
то значение выражения 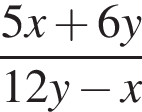 равно:
равно:
Прямая a, параллельная плоскости α, находится от нее на расстоянии 4. Через прямую a проведена плоскость β, пересекающая плоскость α по прямой b и образующая с ней угол 60°. Найдите площадь четырехугольника ABCD, если A и B — такие точки прямой a, что AB = 2, а C и D — такие точки прямой b, что CD = 3.
Известно, что наименьшее значение функции, заданной формулой y = x2 + 8x + c, равно −5. Тогда значение c равно:
На рисунке изображены две окружности с центрами в точках A и B. Если MK = 48, то сумма радиусов этих двух окружностей равна:
Используя данные рисунка, найдите длину стороны AB треугольника ABC, если AM − BM = 2.
Площадь боковой поверхности цилиндра равна ![]() и его объем равен
и его объем равен ![]() Найдите высоту цилиндра.
Найдите высоту цилиндра.
Строительные бригады №1 и №2 купили соответственно 18 и 19 фундаментных блоков у одного из трех поставщиков, выбрав для себя наиболее дешевый вариант. Стоимость одного блока и условия доставки всей покупки приведены в таблице. Определите, на сколько рублей дороже обошлась эта покупка с доставкой одной из бригад. Ответ запишите в рублях.
| Поставщик | Стоимость (тыс. руб. за 1 шт.) | Стоимость доставки (тыс. руб. за всю покупку) | Специальное предложение |
|---|---|---|---|
| 1 | 205 | 1850 | — |
| 2 | 240 | 1950 | Доставка со скидкой 50 %, если сумма заказа превышает 4,5 млн. бел. рублей |
| 3 | 275 | 2050 | Доставка бесплатно, если сумма заказа превышает 5 млн. бел. рублей |
Витя купил в магазине некоторое количество тетрадей, заплатив за них 72 тысячи рублей. Затем он обнаружил, что в другом магазине тетрадь стоит на 2 тысячи рублей меньше, поэтому, заплатив такую же сумму, он мог бы купить на 6 тетрадей больше. Сколько тетрадей купил Витя?
Найдите произведение всех целых решений неравенства 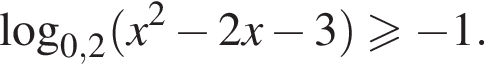
Известно, что при a, равном −3 и 2, значение выражения 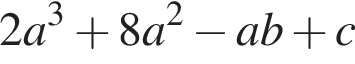 равно нулю. Найдите значение выражения b + с.
равно нулю. Найдите значение выражения b + с.
Найдите периметр правильного шестиугольника, меньшая диагональ которого равна ![]()
Выберите все верные утверждения, являющиеся свойствами нечетной функции ![]() определённой на
определённой на  и заданной формулой
и заданной формулой 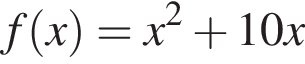 при
при ![]()
1. Функция имеет три нуля.
2. Функция убывает на промежутке [6; 9].
3. Максимум функции равен 25.
4. Минимальное значение функции равно -25.
5. 
6. Функция принимает отрицательные значения при 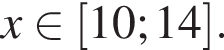
7. График функции симметричен относительно оси абсцисс.
Ответ запишите в виде последовательности цифр в порядке возрастания. Например: 123.
Три числа составляют геометрическую прогрессию, в которой ![]() Если второй член прогрессии уменьшить на 8, то полученные три числа в том же порядке опять составят геометрическую прогрессию. Если третий член новой прогрессии уменьшить на 25, то полученные числа составят арифметическую прогрессию. Найдите сумму исходных чисел.
Если второй член прогрессии уменьшить на 8, то полученные три числа в том же порядке опять составят геометрическую прогрессию. Если третий член новой прогрессии уменьшить на 25, то полученные числа составят арифметическую прогрессию. Найдите сумму исходных чисел.
Для начала каждого из предложений подберите его окончание 1-5 так, чтобы получилось верное утверждение.
A) Значение выражения 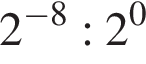 равно:
равно:
Б) Значение выражения 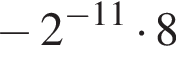 равно:
равно:
В) Значение выражения 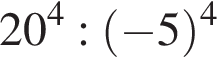 равно:
равно:
1) 256
2) −256
3) ![]()
4) ![]()
5) 32
Ответ запишите в виде сочетания букв и цифр, соблюдая алфавитную последовательность букв левого столбца. Помните, что некоторые данные правого столбца могут использоваться несколько раз или не использоваться вообще. Например: А1Б1В4.
Решите уравнение 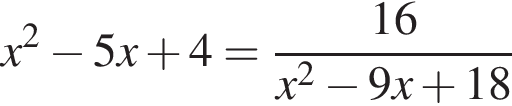 и найдите сумму его корней.
и найдите сумму его корней.
Найдите сумму корней (корень, если он единственный) уравнения 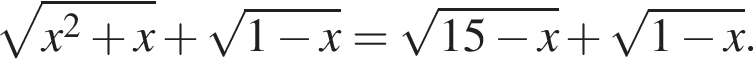
Найдите сумму корней уравнения 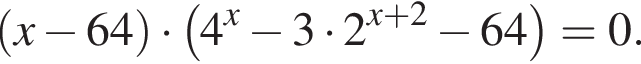
Найдите значение выражения 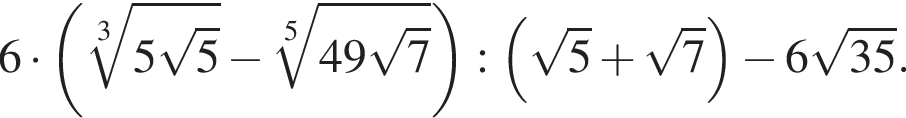
Найдите сумму целых решений неравенства 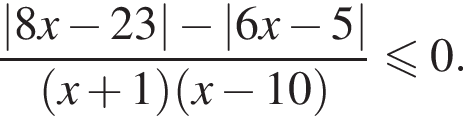
Пусть 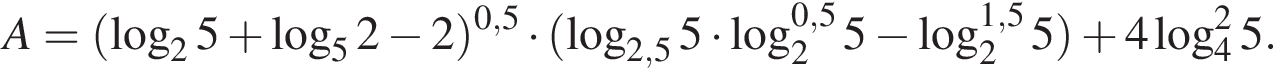
Найдите значение выражения 2A.
На рисунке изображен график функции
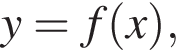 заданной на промежутке
заданной на промежутке 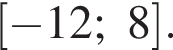 Найдите произведение значений аргумента, при которых
Найдите произведение значений аргумента, при которых 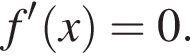 (Черными точками отмечены узлы сетки, через которые проходит график функции
(Черными точками отмечены узлы сетки, через которые проходит график функции 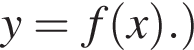
Найдите значение выражения 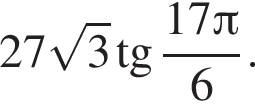
Найдите сумму всех целых чисел из области определения функции 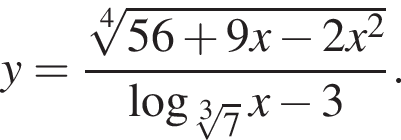
Найдите (в градусах) наименьший корень уравнения
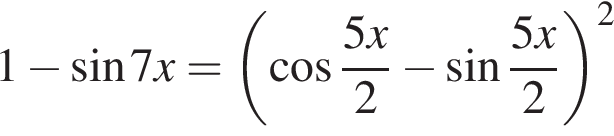
ABCDA1B1C1D1 — куб, длина ребра которого равна ![]() Сфера проходит через его вершины В и D1 и середины ребер BB1 и CC1. Найдите площадь сферы S, в ответ запишите значение выражения
Сфера проходит через его вершины В и D1 и середины ребер BB1 и CC1. Найдите площадь сферы S, в ответ запишите значение выражения ![]()
Равнобедренная трапеция с основаниями длиной 5 и 1 и острым углом 60° вращается вокруг прямой, содержащей ее боковую сторону. Найдите объем тела вращения V и в ответ запишите значение выражения ![]()

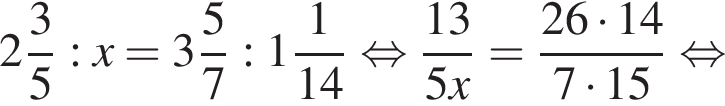
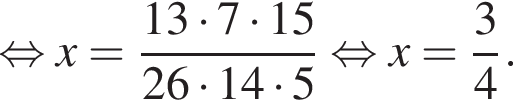
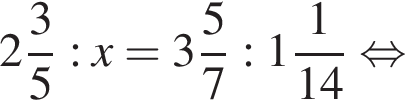
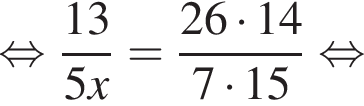
 Тогда получаем:
Тогда получаем: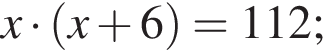
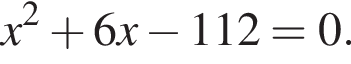
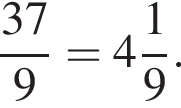
 и при
и при 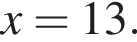 Натуральными решениями являются числа 1, 2, 3, 4, 5, 6, 13. Их сумма равна 34.
Натуральными решениями являются числа 1, 2, 3, 4, 5, 6, 13. Их сумма равна 34. Тогда получим:
Тогда получим: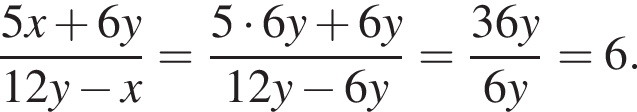
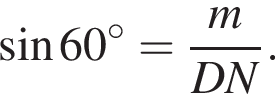
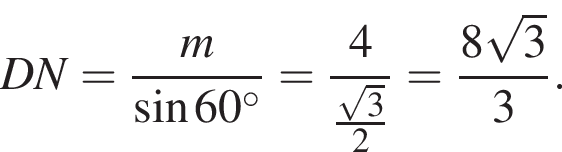
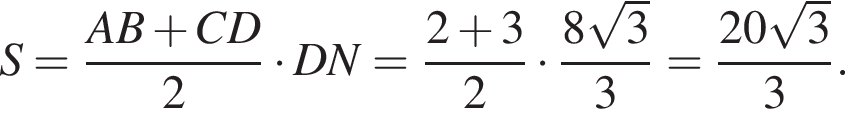
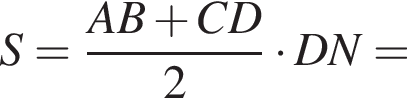
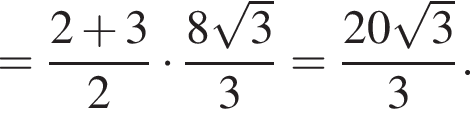
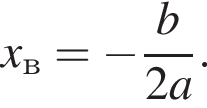 Поэтому
Поэтому 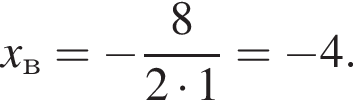 Поскольку y(xв) = −5, имеем:
Поскольку y(xв) = −5, имеем: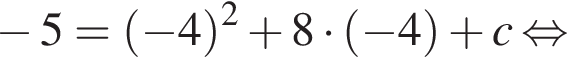

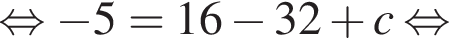
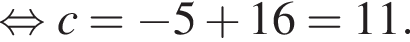
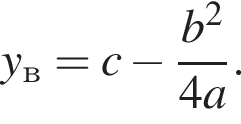
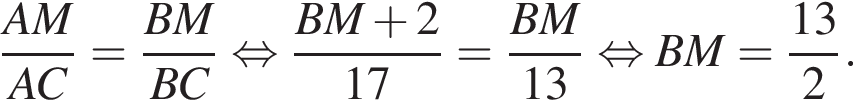
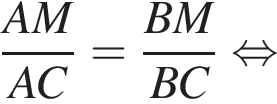
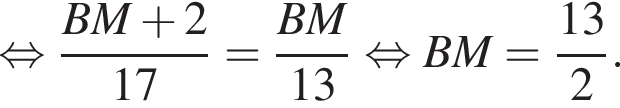
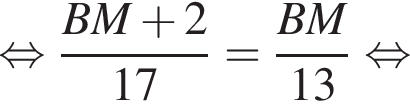
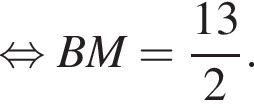
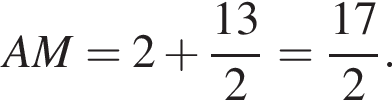 Значит,
Значит, 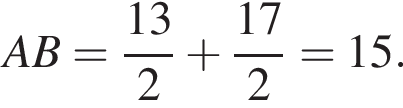
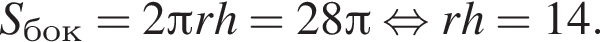
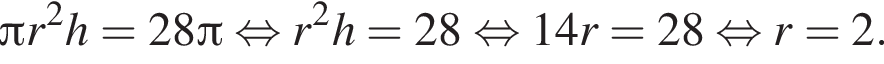


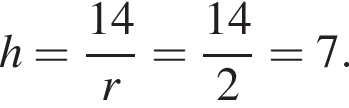
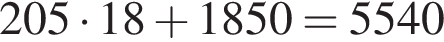 тыс. руб.
тыс. руб.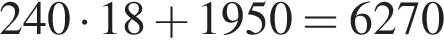 тыс. руб.
тыс. руб. тыс. руб.
тыс. руб. тыс. руб.
тыс. руб. тыс. руб.
тыс. руб. тыс. руб.
тыс. руб. Если бы Витя купил тетрадь в другом магазине, то было бы верно равенство
Если бы Витя купил тетрадь в другом магазине, то было бы верно равенство 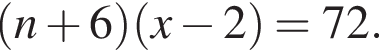 Решим систему уравнений:
Решим систему уравнений: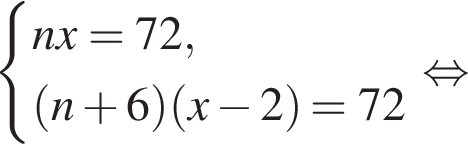
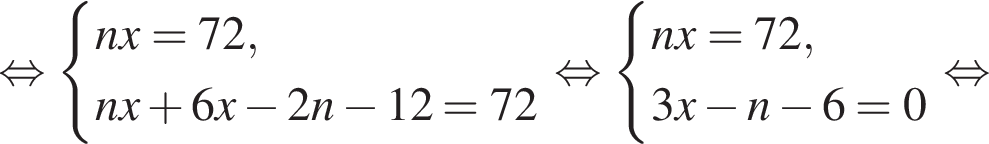
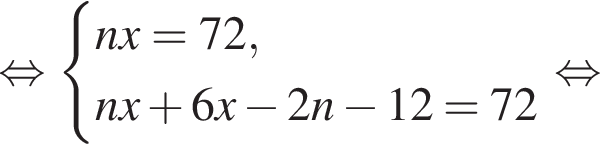
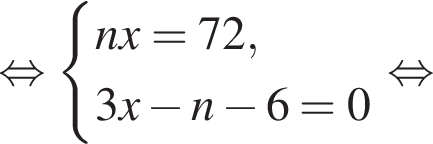
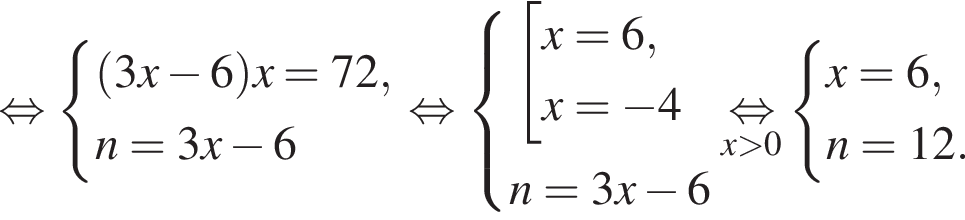
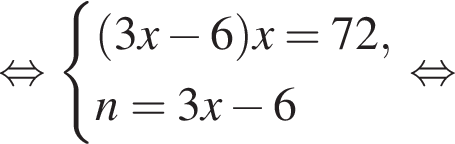
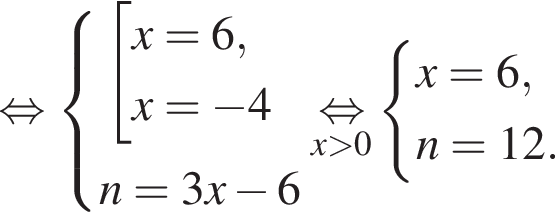
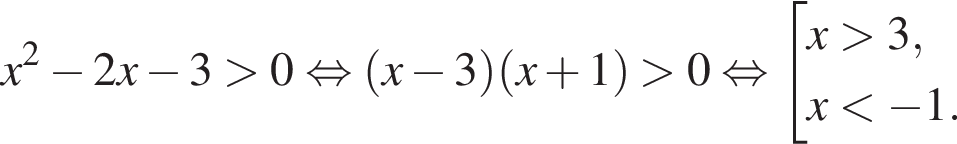
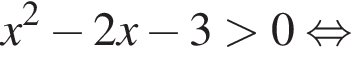
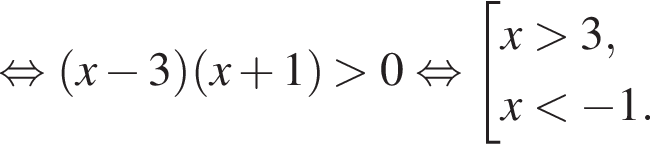
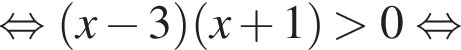
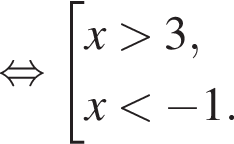
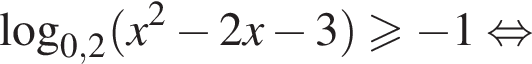
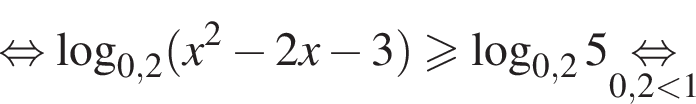
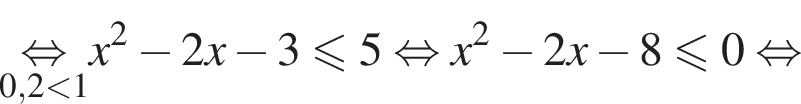

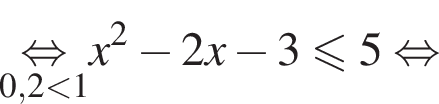
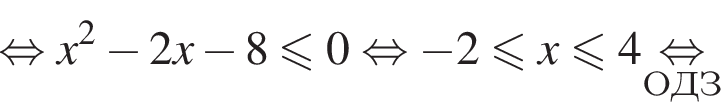
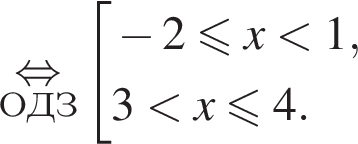
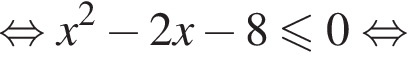
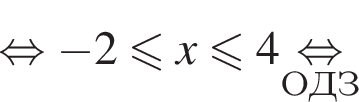
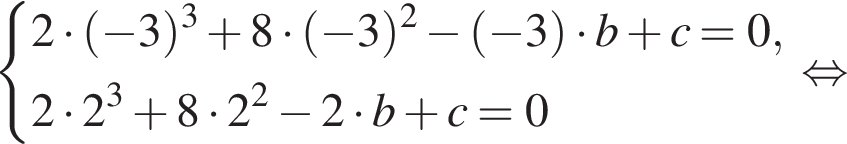
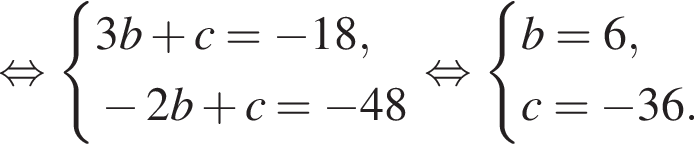
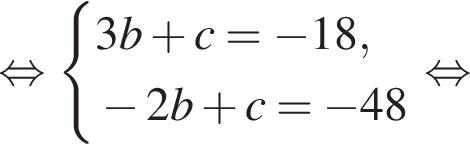
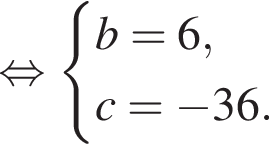
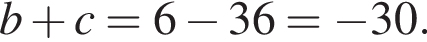
 при
при 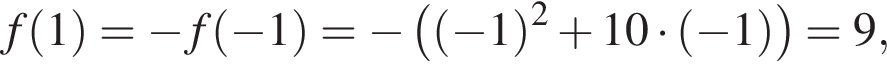
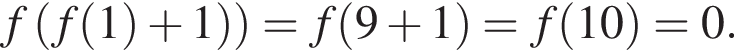 Утверждение 5 верно.
Утверждение 5 верно. функция равна нулю, а значит, принимает отрицательные значения не во всех точках отрезка
функция равна нулю, а значит, принимает отрицательные значения не во всех точках отрезка  Утверждение 6 неверно.
Утверждение 6 неверно.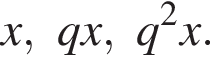
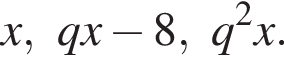
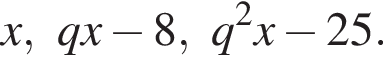
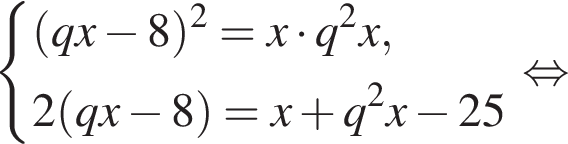
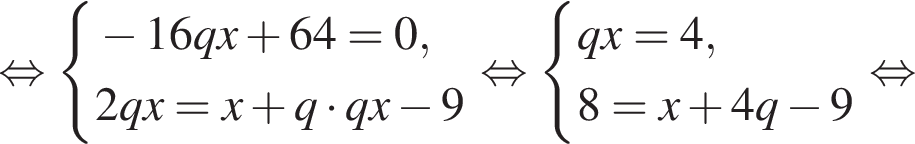
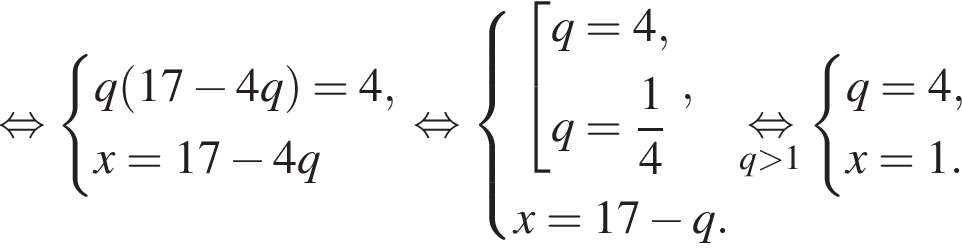
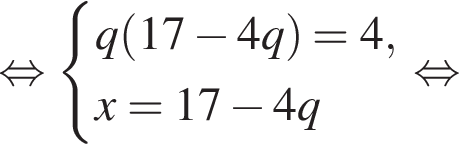
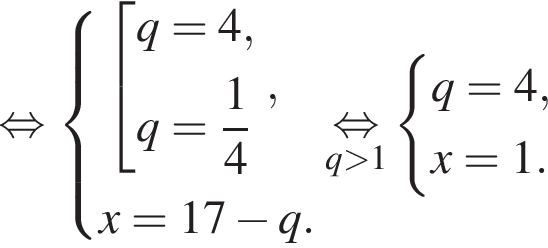
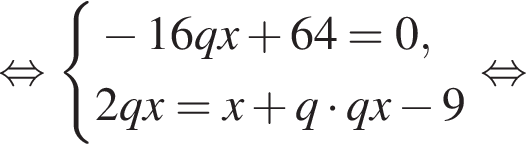
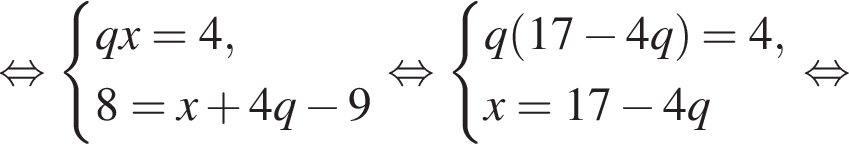
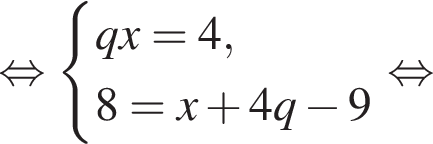
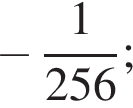
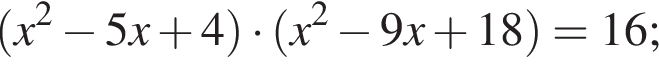


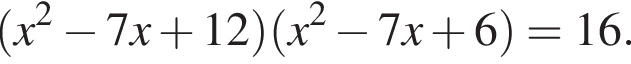
 Получим:
Получим: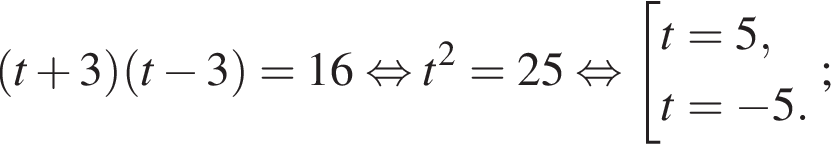
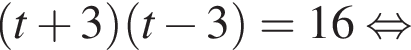
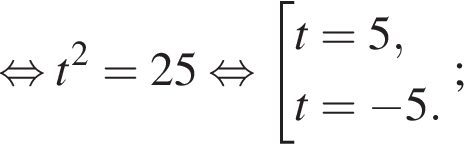
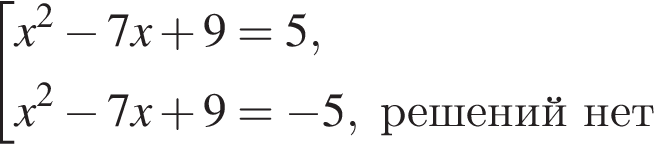
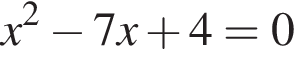 найдем по теореме Виета, она равна 7.
найдем по теореме Виета, она равна 7.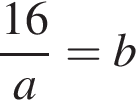 равносильно уравнению
равносильно уравнению  искать ОДЗ не требуется.
искать ОДЗ не требуется.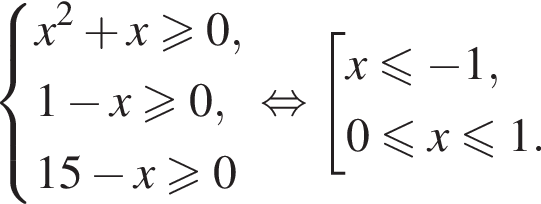
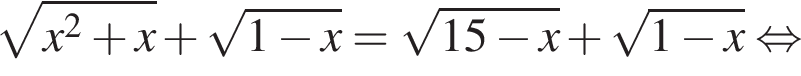
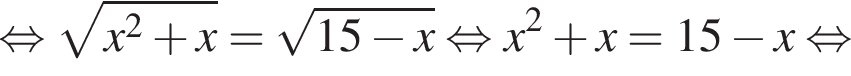
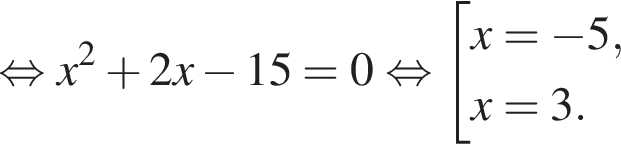
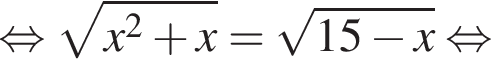

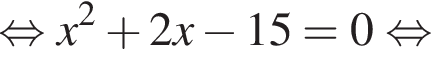
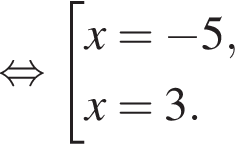
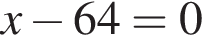 следует, что первый корень
следует, что первый корень  Рассмотрим
Рассмотрим 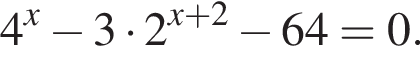 Сделаем замену
Сделаем замену 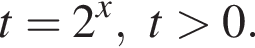 Тогда:
Тогда: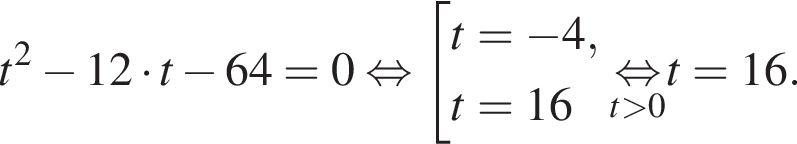
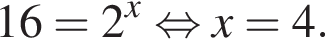 Отсюда следует, что сумма корней уравнения равна 68.
Отсюда следует, что сумма корней уравнения равна 68.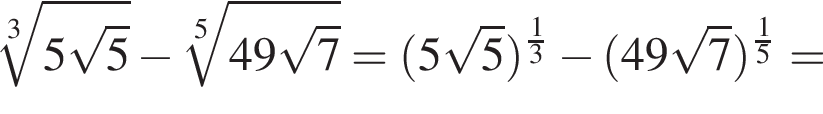
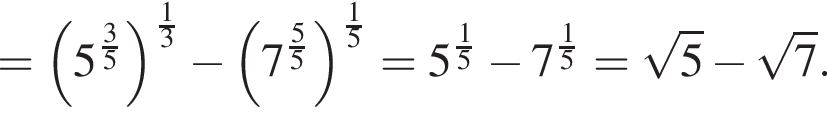
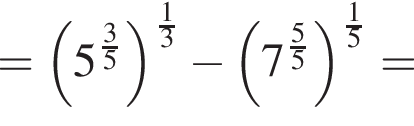
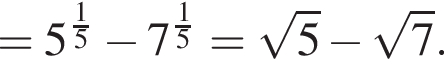
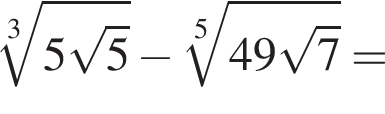
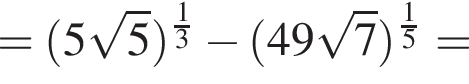
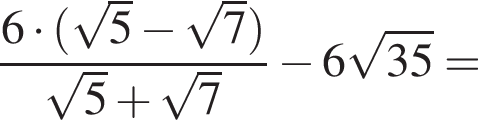
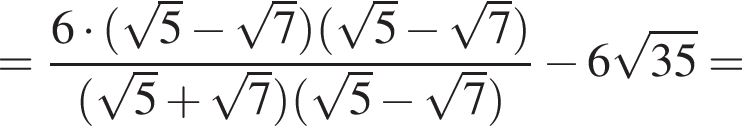
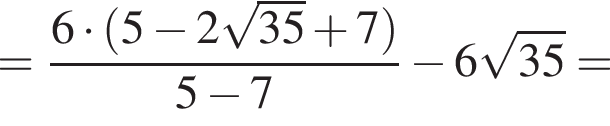
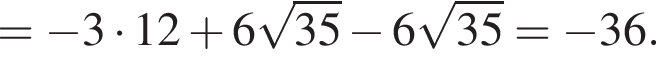
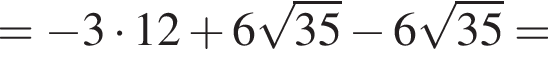
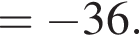
 совпадает со знаком разности
совпадает со знаком разности  имеем:
имеем: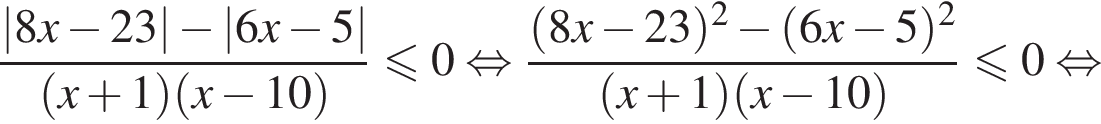
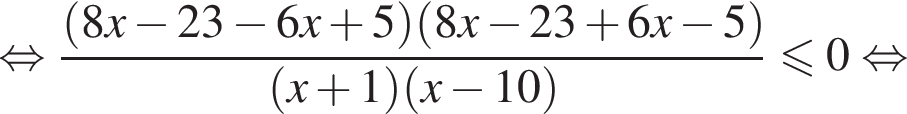
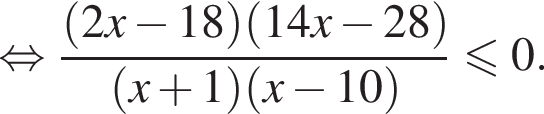
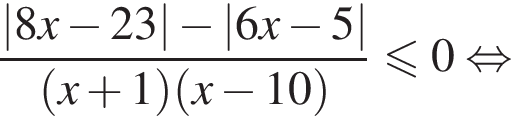
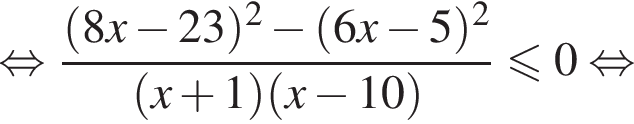
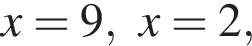 корни знаменателя
корни знаменателя 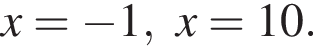 Поэтому:
Поэтому: 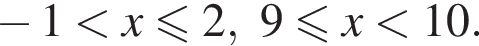 Целые решения — числа 0, 1, 2, 9. Их сумма равна 12.
Целые решения — числа 0, 1, 2, 9. Их сумма равна 12.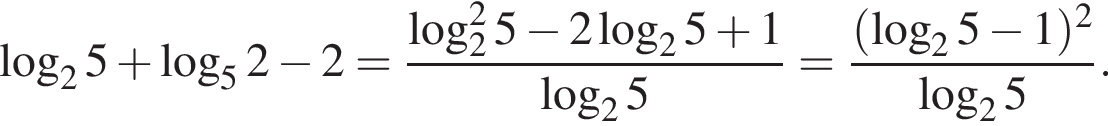
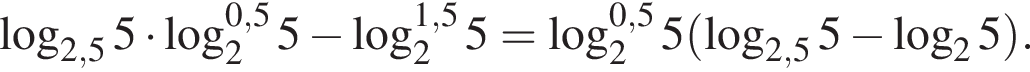
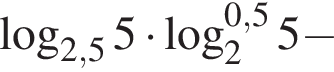
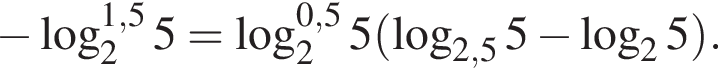
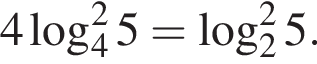 Тогда имеем:
Тогда имеем: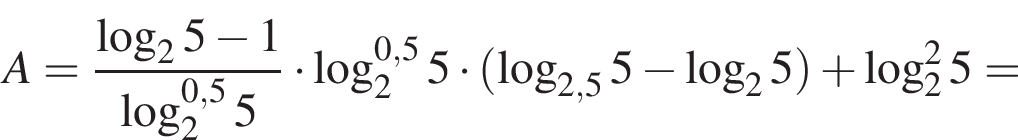
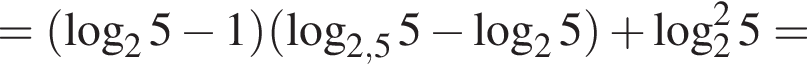
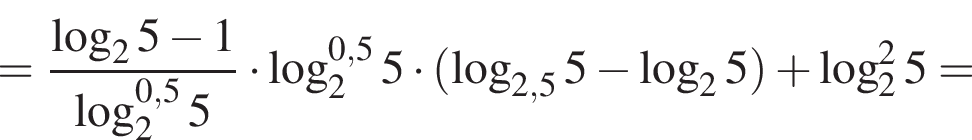
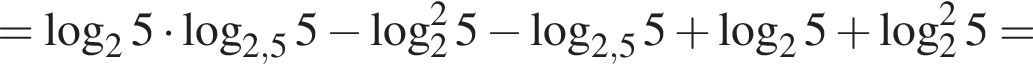
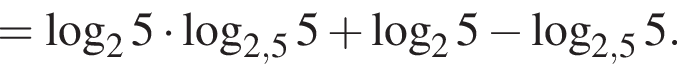
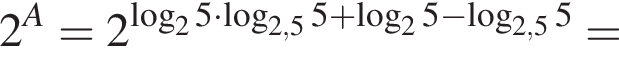
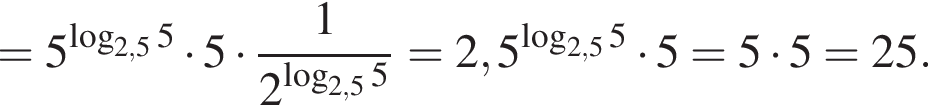
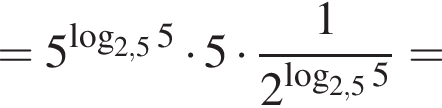
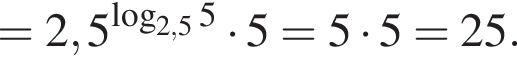
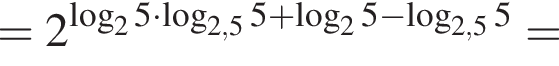
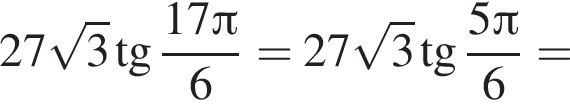
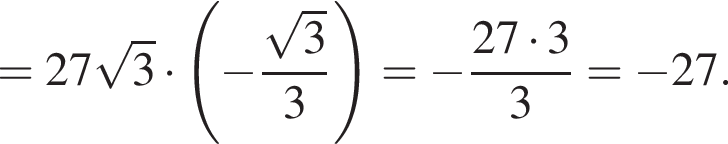
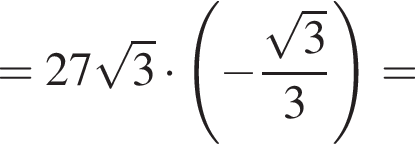
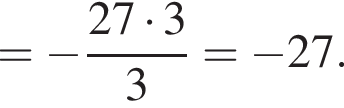
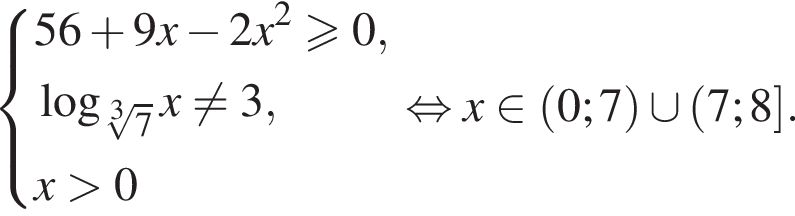
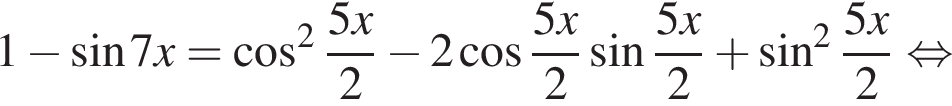
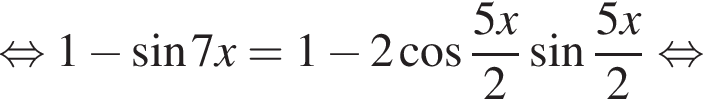
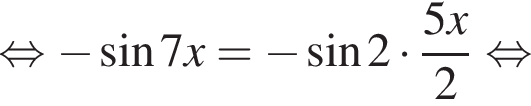
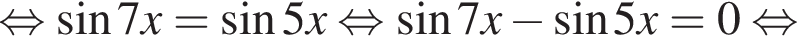
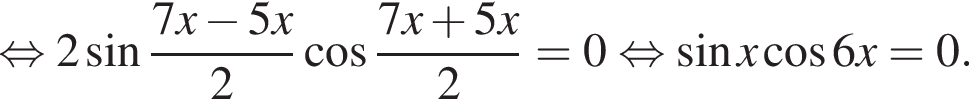
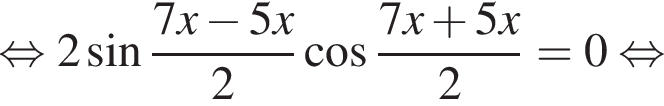



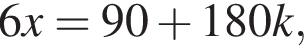 где k целое, то есть при условии
где k целое, то есть при условии 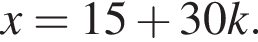 При k = −6 получим
При k = −6 получим  а при
а при 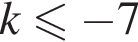 получим
получим 
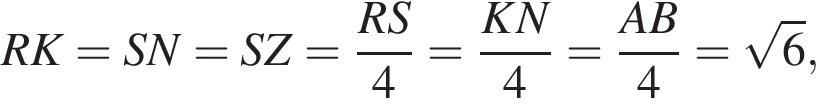
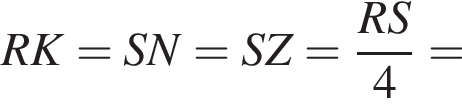
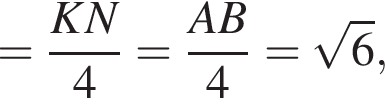
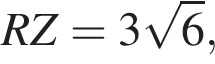
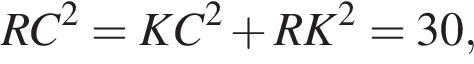
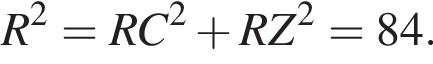
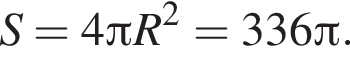
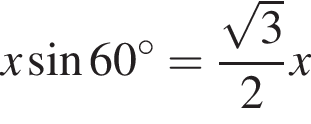 и потому объем двух таких конусов равен
и потому объем двух таких конусов равен